numbers

by

My way of life is blogg’d into the sere, the yellow leaf

Hello and good morning.

TTFN

Ha.  Ha.  Sorry about that.  Just, honestly, I don’t really feel much like writing right now.  There are no other twos here today (at least, I’m not going to be talking about them, except to the extent that saying that I’m not talking about them constitutes talking about them).

Actually, wait.  I will make a relatively fun note that includes the number two, since it just occurred to me that today is the fifth:  If you add (or if anyone else adds) the first two prime numbers together, they give you the third one.  2 + 3 = 5.

This is the only place in all the infinite realm of the prime numbers in which you will be able to add two consecutive primes to get the next prime, because all prime numbers except two are odd, and if you add (or anyone else adds) two odd numbers together, you (or they or he or she) will get an even number.  And the only even prime is two.

Actually, it’s worth noting that one can add two primes that are not consecutive to get a third prime.  If one takes any of the first member of a set of twin primes* and adds two (that solitary even prime) to it, one will get the second of the pair of twin primes.  This may be able to be done in an infinite number of cases; it’s thought that there are an infinite number of twin primes, i.e., that there is no largest twin primes set.

However, this has not been proven yet (as far as I know) though work has been done on it and progress has been made.  I won’t get much more into it than this, except to say that apparently a lot of the work has been done by large, decentralized groups of mathematicians (professionals and amateurs) through a site called “polymath”, if my memory is correct.

Now that is an excellent name for a collaborative mathematics website.

Oy, there I go again, talking about trivia about prime numbers and so on.  Maybe it would make sense for me to get into these things if I were truly involved, but I’m a spectator of mathematics (apart from my truly useless invention of the gleeb**, a number which, when multiplied by 0 gives you 1).  So my interest is entirely esoteric and reflected.  I apologize to those of you who find it tiring.  To those of you who like it, I’ll say “You’re welcome”.

You’re welcome.

See, I told you I would say it.  And then I said it.  I guess that’s one point in my favor.

I’m not sure there are any others.  At least, none of them appear to me to be in my favor.  I am all but completely worn out.  I’m running on fumes, or whatever other metaphor one might want to apply that is applicable (since applying inapplicable ones is stupid) and my incessant pain continues to wear me down, adding to my depression, and eroding what little joy I have left.

I really have wanted so often just to hang it up.  I came relatively close yesterday afternoon and considered leaving a “post” that just said, “I don’t think I can do this anymore.”  The would be the title and the content.

I didn’t do it, of course, which you can tell by looking, if you are so inclined***.  But I came closer than I’ve come before, at least subjectively speaking.  Last week—I think it was—I posted a similar sentence on most of my social media, just the line “I don’t know if I can do all this much longer.”  I’ll embed a screen shot here:

 

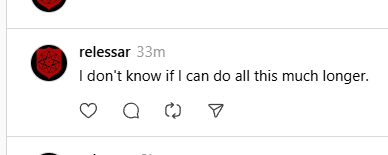
So, fair warning is being given, here and elsewhere.  The fire alarm is giving off little warning beeps.  The readout dial is high in the yellow range, perhaps already inching into the red.  Creaking sounds and little wisps of steel and concrete dust are issuing from the support beams of the bridge.  Small tremors and puffs of escaping steam are increasing in frequency near the hitherto dormant volcano.  There’s a red sky in the morning, today****.

But, I appear not to be able to stop yet.  I’m not yet able to escape.  I’m still pushing the stupid boulder up the stupid hill, like the stupid idiot that I am.  I’m even writing this blog post on my lapcom for the first time in two weeks (well, this is the first time at all that I’m writing this blog post, but hopefully you know what I mean), just because I felt mildly nostalgic.

One of these days, though, I’ll be able to end my blog post with just “TT” instead of “TTFN”, and it won’t be over just for now but finally and for good—not just the blog but everything.  And I don’t know if that will be sad or a relief for anyone out there, but I hardly think it will be a tragedy, nor will it be more than little noted, and it will certainly not be long remembered.

But for now, I must needs sign off with the annoyingly non-climactic

TTFN

*Primes that are two apart from each other, such as 29 and 31, or 137 and 139.

**Seriously, I worked out a lot of the algebra that involves it and everything (for instance, it turns out that a gleeb squared is still a gleeb, and 1 over a gleeb equals 0).  I’m sure I discussed it in a previous blog post.  If I can find which one without much trouble, I’ll leave the link here.

***In principle, you can tell by looking even if you are not so inclined, but you simply will not tell because you won’t look.  Should that count, then, as a “can” situation if it’s not physical impossibility but mental disinterest that leads one never to do a thing?  If it simply will not ever happen, can one not just then say that it cannot happen?  Are “cannot” and “shall not” synonymous here, as when Ian McKellen misspoke his most famous line when facing the balrog in The Fellowship of the Ring?

****This may be true somewhere—it probably is, come to think of it—but it’s not true for me, because it’s still fully dark as I write this; the sun is not even lightening the eastern horizon yet.  I’m just being melodramatic.

by

どうも ありがとう Mister ロバあと

It’s Wednesday the 4th of February (02-04-2026 in the US).  The best I can currently think of to say about today’s date is that it is composed entirely of even digits‒twos, zeroes, a four, a six‒which is at least uniform in a sense.  But it’s rather boring, too.

Admittedly, most people probably find any such evaluation of dates with respect to numerical patterns boring.  I would apologize, but it’s not as though anyone is forcing anyone else to read my blog.  If someone were doing so (and I wouldn’t necessarily try to stop them), I’d like to think I would have a far larger circulation than I have.

As it is, my circulation is roughly 5 liters.  Ha ha.  That’s a (lame) joke regarding the volume of blood in a typical adult human body.

While I may not feel as though I am a member of the same species as most humans, I recognize that my gross physiology is basically the same, and so my blood volume should be comparable.  My body just doesn’t seem to work quite as well as that of the average person, at least in some senses.  For instance, my chronic pain has continued to attack me with exceptional aggression over the past several days; yesterday was particularly bad, and today is not shaping up well so far.

Not that this is anything new.  I’ve been in chronic pain every day for a quarter of a century now (though I suppose when it had just begun one would not call it “chronic”), if my memory is accurate, which it usually is.  That’s just a bit longer than my youngest has been alive.  It’s not pleasant (though my youngest is), and at least partly in consequence of my chronic pain, neither am I.

I do think that my outlook and my personality would be much better if I did not have pain every day.  I would probably sleep better, as well.  I almost certainly would not have gotten involved in trying to treat other people’s chronic pain in less than ideal circumstances, and so would have avoided at least some catastrophes that happened because of that (apparently misguided) intention.

Still, I’ve been prone to depression since I was in my early teens, well before the onset of my chronic pain, so maybe I’ve always been unpleasant.  And though I didn’t know it, I’ve had ASD all my life (even after the heart-based ASD I had was corrected through open-heart surgery when I was 18).

That’s a weird coincidence of acronyms, isn’t it, those two kinds of ASDs in one person*?  It can be rather confusing when the same acronym signifies two quite different things.  Still, there are only so many 3-letter acronyms available.  The maximum number in English is 26 to the 3rd power, or 17,576.

You might think that ought to be more than enough for there to be no overlap, but of course, acronyms aren’t merely randomly chosen letters.  They need to signify something specific in order for them to be useful, and far more words start with A or S or D, for instances, than start with X or Z or Q.

It’s a bit like dealing with words in general.  In principle, a word of a particular length (let’s use the variable x to signify that length) in English could be any one of 26 to the xth power possibilities.  But English is not a random cipher, and there are many possible orderings of letters than are not “allowed” in English, because they don’t produce any plausible sound.  English is, of course, a written version of a spoken language.  If a word can’t even be pronounced, it’s not much of a word.

One cannot, for instance, have a word that consists of all consonants (certainly none are coming to my** mind).  One could produce strings of consonants that could be sounded out, I suppose; one could for instance pronounce the string “mrndl” pretty readily, I think.  But that’s just generally unwieldy, and in some languages it cannot be done.

In Japanese, for instance, all but one pair of kana representing sounds/syllables (hiragana for native words, katakana for imported words) are of the “consonant-vowel” sound type (e.g., ha, ke, ni, su, to, etc.) or just vowels (e.g., a, i, u, e, o).  Only the “n” syllable stands alone (sometimes pronounced as almost “m” depending on the context) and it occurs only at the ends of words.  Thus, in the game of shiritori***, if a player says a word that ends with “n”, they lose, because the next person cannot possibly begin a subsequent word.

How did I go from discussing the uninteresting digits of today’s date to the game of shiritori?  I suppose I’ll find out when I do my editing.  It is strange, though, even to me.  I can only imagine how bizarre and confusing it must be for others to read my blog posts.  With that in mind, I’ll cease this particular crime against humanity or against logic or reason or whatever for now.  Please accept my apologies, and hopefully you will have a good day.

[P.S. The above headline would be transliterated as “Doumo arigatou, Mister Robaato”, which can be meant as “Thank you very much, Mister Roboto” (as in the Styx song) or as “Thank you very much, Mister Robert.”  Curious, ne?]

*Actually, there is a higher incidence of cardiac ASDs, as well as several other atypia that I have (such as a cavum septum pellucidum) in people with the neurodevelopmental version of ASD than in the neurotypical population.  Interesting, isn’t it?

**Wait a moment‒the word “my” is superficially composed of two consonants, isn’t it?  Well, in a sense that’s true, but this is one of those cases we were taught about in elementary school in which the letter “y” acts as a vowel.

***(しりとり)  In this game, one person says a word, and the next person has then to say another word that begins with the same syllable with which the previous word ended.  It goes on until one player cannot think of a word that hasn’t already been used or until someone uses a word ending with “n”.

by

Is it possible for there to be too many twos on a Tuesday (in month 2)?

It’s Tuesday the 3rd of February today.  It would have been better if Tuesday was the second of February, because then there would have been many numeral twos in today’s date to go along with the rhyming “tue” in the day’s name.

Actually, you know what, let me check something…

…nope, the 2nd of February in 2022 fell on a Wednesday, it seems.  Oh, but wait.  2-22-2022 did fall on a Tuesday!  I can’t believe I didn’t remember that fact, nor do I remember that day.  I’m slightly ashamed of myself for that.

Well, at least this month started on a Sunday, which means it will have a Friday the 13th.  That’s not going to be this Friday, of course‒that will be the 6th, which is inescapable when Tuesday is the 3rd‒but the next one.

Oh, and this is a non-leap-year February, and thus has only 28 days (which is exactly 4 weeks).  That means that March will also have a Friday the 13th, since it too will start on a Sunday.  That’s pretty much as good as it gets with respect to Friday the 13ths; this is the only situation (in our current date-reckoning system) in which we can get two months in a row with Fridays the 13th.  So, huzzah!

It doesn’t actually matter, of course; I attach no mystical significance, good or bad, to any particular kind of date (even a first date, which is something I haven’t experienced in at least a decade and a half).  I just think it’s amusing to celebrate and enjoy a date that is a prime number (my favorite prime number) and of which some people in the west have a bizarre superstitious fear.

Indeed, the fear of that date is so real but so absurd that there’s a whole quite silly and famous series of slasher movies which went by that name.

Thinking about the Friday the 13th movies makes me think about the peculiar stochasticity of creative franchises.  The first of those movies had as its villain (spoiler alert!!) the mother of Jason; she was killing camp counselors as a sort of displaced revenge against the counselors who had been having sex while her son (Jason) drowned* in Crystal Lake while swimming unsupervised.

One might think she would accept some responsibility, herself.  If she’d raised the stupid little fuck even half competently, he might have known not to swim in the lake unsupervised.

And where the hell was she anyway?  She worked for Camp Crystal Lake, supposedly.  When the “drowning” occurred, it was clearly not a regular camp session, or there would have been other kids around, at least.  And the counselors would be unlikely to be having sex in the middle of the day while a bunch of other kids were around.  I suppose it’s possible Jason snuck out at night, in which case:  he was the one most directly responsible, but his mother should have raised him better and should have been keeping an eye on him.

I’m taking this too seriously, I know.  But I do hate when people seek revenge on, or simply blame, a type of person rather than the actual specific person or people who did them wrong.  It’s not that I think that revenge is always a mistake; there are clearly evolutionary reasons why people are prone to take revenge against (perceived) wrongdoers.  Still, that tendency evolved in humans (or their ancestors) that lived in relatively small groups where everyone knew each other, so who did what was usually pretty clear and specific.

However, to hold some group of people to task who are merely similar in some way to someone who (from your point of view) did you wrong is not merely morally reprehensible, it is intellectually indefensible, and as a matter of character it is just pathetic.  It’s very much just another kind of bigotry, and all bigotry is a profound and contemptible intellectual and moral failure, no matter by whom and in which direction.

But I digress.  I was making a point about how franchises evolve from their starting points if they go on for very long (if I remember correctly).

By the second installment of the Friday the 13th movies, Jason‒the boy (?!) who supposedly drowned‒was somehow now the killer, and he wore a burlap sack mask.  Then in the 3rd movie (in 3D!) he took from one of his victims the hockey mask that became his trademark.  And so it went.

I suppose it’s not surprising that a franchise made by lots of different people over many different years should evolve over time.  But even when something creative is done entirely by one person, things can change in interesting ways that would not necessarily be predictable, certainly in their specifics, ahead of time (and it’s more or less by definition impossible to predict something after the fact).

I’ve mentioned this happening with comic strips, citing the examples of Peanuts and Calvin & Hobbes, both of which showed striking differences as they matured from their initial, raw forms.  Likewise, the Discworld books by Terry Pratchett developed into much more sophisticated and interesting novels over time (though even the first ones were very good and very funny).

Of course, we’ve all seen this happen to long-running TV shows, some of which initially grow and become more complex only to “jump the shark”** in the end, others of which mature into things of real quality, like Star Trek: The Next Generation, after somewhat uneven beginnings.

And, speaking of things jumping the shark, I don’t even remember if I had a coherent idea for this blog post, but if I did, it’s gone now (and my blog overall has certainly morphed from its original form and intention).  So, given that, I’ll bring this post to a close before I embarrass myself even more than I usually do.

I hope you all have a good day, for whatever such hopes are worth.  I suspect they’re not really worth very much, but then, neither am I.

*Though he was somehow alive for the sequels and was a grown man with bizarre deformities.  But if he was alive, and had been alive (since he had supposedly been a boy when he “drowned” but was fully grown in the remaining movies), then why was his mother so pissed off?

**Literally, in at least one case.

by

I’m having difficulty coming up with a headline

Well, it’s Monday, 1-26-2026 (in the American ordering of dates), a sequence which is mildly but not very interesting because of the repeated “26”.  Now, come February 26th, writing the date in the more European fashion would be 26-02-2026, which will be almost palindromic, but not quite.  So that would be a sort of tease date, in a way.

None of it matters, of course.  Now, if there were a 62nd of February I would be somewhat tickled on that day.  Of course, in a way, you could say that the 3rd of April is the 62nd of February, if my math is correct.  I think that’s right.  Let’s see, there are 28 days in February (no more than that this year), then 31 days in March, which adds up to 59 days.  Then 3 more days will get you 62, so yeah, April 3rd.

Sorry, I know that’s probably terribly uninteresting to anyone but me.  A lot of things are like that.

I was able to get a decent night’s sleep on Saturday night by sedating myself with a combination of three (or so) different (legal and “over the counter”) medications.  Of course, I cannot do that on a weeknight or I will be useless the next day*.

Not to say that I’m particularly useful at any other time, but at least I can think with some clarity.  My emotions may tumble about‒though evidently they rarely if ever show on my face‒but at least I have a sharp mentality most of the time.  In fact, if I were able to bring myself into more durable focus, I think I could be more mentally acute than I’ve ever been in the past.

That’s because, although I’ve been through a lot of failures over time, I am at least always trying to learn, and I succeed in that quite often.  Whether or not I learn the things that are most interesting and/or most useful is another question.  But it’s hard to know for sure ahead of time what will be most useful to know, so it’s probably best to try to learn as much, about as many things, as well as you possibly can.

That’s probably as wise as I ever get.  Enjoy.

Let’s see, what else should I talk about?  I don’t know.  Is there anything you’re interested in discussing?  Do you have any questions for me that you would like answered**?

I suppose today I shall have to deal with the new format for entering the blog onto WordPress, which is somewhat irritating, because it is more difficult to read as I’m editing, and it is less user friendly.  I am at least half heartedly considering moving my blog to Substack (or something).  I have an account there, anyway, and quite a few of the people whose ideas interest me seem to publish there.

It’s a bit of a no-frills site, where you don’t make your page into a fancy-looking thing, you just publish your stuff, but it has its own sort of built-in social media thing where you can make the equivalent of tweets and respond to those of other people.  And, of course, it has a built-in capacity to set up paid subscriptions for people who want them, and one can choose which things are paywalled and which are not.

To be fair, WordPress has that capacity now, as well, but I’ve never seen it used nor looked too much into using it.  If any of my readers know about it and how it stacks up against other things, such as Patreon (and Substack) please let me know about your experience.  I would greatly appreciate it.

Of course, this is all pie in the sky thinking on my part.  I doubt that anyone cares either way, in any case.  And I don’t know if I’m going to crash and burn sometime in the near future.  I feel that the event is approaching rapidly, but I’ve felt that way often and for a long time, and yet against all odds (and certainly not by popular demand) I am still here.  I’m sort of like the world’s most verbose toenail fungus, in a way.

Anyway, I think this is enough for today.  Again, if any of you have experience with Substack, or with Patreon, or even with the subscription models on WordPress (this site is hosted through WordPress), I would appreciate your feedback.

In any case, I do hope that you have a good day.

*I will not, though, sleep more if I use this on weeknights‒I know this from bitter experience.  Something in my mind overrides even medication (within reason) and still wakes me up stupidly early on any day that I have anything to do, whether it’s work or laundry or what have you.  But the cumulative effects of pharmacological intervention nevertheless dull and slow my mind, so I feel worse very quickly.  Believe me, I’ve tried.

**I make no promise that I will answer just any question you might ask, but I will try to be forthcoming if I can.  I wouldn’t want to discourage someone who is taking an interest; such people are rare.

by

Minding primes and priming minds

It’s Monday the 19th of January (in 2026 CA or AD).  19 is a nice prime number, but it’s one people don’t think about very often.  Stephen King turned it into an “evil” number in his extended universe, which is much less obvious and predictable than using the unjustly maligned number 13.  I’ve always* liked that he did that.  It was clearly chosen at least partly because it was (and remains, and always will be) a prime number.  But it’s not an obvious one.  So, nice job King-sensei (not that he needs my moral support, though I would welcome such support from him).

I occasionally think about mailing Stephen King a copy of one of my books just on the off chance that he might read it some day when he’s bored.  If I were to develop the chutzpah to do such a thing, what do those of you who have read my stories think would be the best one to send him?

Take your time, and don’t be shy.  I’d love to hear from all…what, one of you?  Two?

I don’t think there could be three, but I could be wrong.

Returning to the topic of prime numbers, I had a cool thing happen on Friday:  I bought some stuff at the local convenience store, and my total was $19.07.  I looked at it for a moment and thought that it was a cool-seeming number.  I know 19 and 7 are both prime, and the digits don’t add up to a multiple of 3, nor is the total number a multiple of 4 or 5, obviously.  I wondered if it might be prime.

Back in the day, I would have had to check that more or less manually, but nowadays, I was able just to type into the search bar “Is 1907 prime?”

It is!  Or so claims Google.  If necessary, I could check it myself, by hand, though that would be laborious.  I suppose it wouldn’t be hard to write a quick computer program to check all the possible factors (among numbers less than 954**).  I doubt that I will do either thing, though.  I’m pretty confident in Google on this point.

And now, having said that, I’m starting to feel uncertain.  Could Google be wrong about this?  Am I really going to have to check for myself?

I remember when I realized I had never seen the Pythagorean Theorem proven mathematically (I grew up in a declining school system, sorry).  So, I had to prove it to myself to my own satisfaction, which I did.  Thankfully, it’s easier to prove something like that when the answer (so to speak) is well known.

Okay, enough numeracy, or whatever the best term for the preceding matters might be.

I did not work on Saturday, which is why I didn’t write a blog post on Saturday.  The office was open, but my coworker was able to come in, and the boss specifically told me to take the day off.  Apparently, my exhaustion really was beginning to show, even to other people, which seems not to be the usual case.

Of course, having one day of actual rest doesn’t cure my situation, but it is a minor respite.  I have more fundamental issues than mere rest or lack thereof, but I am not sure there is any way to fix them, at least not in practice.

In principle, of course, it must be possible at least to improve the settings in my brain‒tweak this set of synapses and adjust sensitivity to this or that neurotransmitter, increase (or decrease) the blood flow to this and that region of the brain, etc.  That sort of thing, done precisely and judiciously, could in principle correct or adjust any parameter of brain function one might want, in whatever ways lie within the realm of the brain’s potential.

We’re a long way from being able to carry out such manipulations, and it’s by no means certain that we will exist long enough for neuroscience to achieve such things.  But there’s no principle of nature that precludes it.

Of course, people might be quite leery of even researching such things, even when we finally know enough to do so.  After all, if we can adjust the brain specifically and precisely to make it less depressed or less anxious or less forgetful, we can adjust it in other ways, too.  One could adjust someone’s brain to make them fall in love with a particular other person, like the mythical old magic love potion.  I think most people would rather not fall in love that way (though there’s no reason to think such love would be any less delightful to experience than ordinary, clumsy, stochastic love such as what we have now).

Indeed, one could adjust human minds to make them happy, no matter what the circumstances.  Of course, this could well be used to dominate whole populations of people; one could keep them under constant control because they would be happy, and you could keep them motivated and loyal and satisfied with whatever their lot might be.  I think most people would find that notion repugnant, but it is at least somewhat morally ambiguous, because such people would be as legitimately happy as anyone who becomes happy “on their own”.  Indeed, they might well be happier than any person had ever been before, and more “well-adjusted”, and more creative, and more psychologically healthy.

I get near some of these concerns in my book(s) Unanimity:  Book 1 and Unanimity:  Book 2.  I wouldn’t say those specific ideas figure centrally, though matters of mind and free will and the nature of a person’s character and how it can be changed by physical events are a big part of it.  Also, all sorts of horrible things happen, since it is a horror novel.  And there’s a lot of room for all of it, since it’s as long (total) as the unabridged The Stand and It, to bring us back to Stephen King.

With that, I guess I’ll draw today’s post to a close.  Hopefully, I won’t already be exhausted by tomorrow.  I hope you have a good day.  And if any of you know Stephen King, please ask him which of my books he might think he would want to read.  I’d really appreciate it.

*Well, not always.  I didn’t like it before it happened or before I knew about it.

**Incidentally, 953, which is the rounded-down answer to 1907 divided by 2, is also a prime number.  That’s kind of nice.

by

“The numbers don’t decide”

I don’t have any fun numerical trivia to notice about the numbers of the date today, which is Wednesday (1-14-2026), by the way.  It’s not that I’m saying there are no potential fun numerical comparisons or patterns or what have you in the numbers of the date today, just that there aren’t any that stuck out for me, which probably means that there aren’t any which I would think are fun.

Prime numbers and palindromic numbers are probably my favorites of these kinds of things.  But although the primes are considered the “atoms” of the number world by those who study such things specifically—I guess those would be number theorists—there are many situations in which there are no obvious prime numbers.  I suppose the same is true of actual atoms, come to think of it.  When was the last time you encountered a single, naked atom in the wild, so to speak?

Anyway, I’m not really interested in “talking” about that right now.  I’m not really all that interested in much of anything.  I know, I know, this is getting ridiculous, I keep writing one relatively upbeat or at least engaged* post, and then I turn somber and negative on the next one.  Well, rest assured, in case you weren’t already, I feel generally glum and somber during the day even on those days when I write posts in which I’m truly interested, like yesterday’s.  You just have the good fortune not to be around me.

Even among those who are around me, such as the people at work—actually, there’s no “such as”, these are the only people around me except on truly rare occasions—there’s probably not much of a clue as to my glumness.  Apparently, my moods and feelings don’t show on my face, even when I become aware of them consciously, which can tend to be rare (I appear to have a degree of alexithymia).

So, even when I feel that I’m not sure I can make it through the rest of a given day, let alone through any more significant time, no one seems to notice.  There are and have been people at the office who have dealt with drug and alcohol problems, legal issues, erratic life choices, sporadic attendance, stuff like that, and they get at least tacit moral support and even help; there are various resources in the community to assist them that are readily available, and our culture lionizes those who recover from drug problems, even as often as they might backslide.

I just have a dysfunctional brain, or so it seems, and the useful resources to help that (without insurance) are about as prevalent as icicles in Death Valley.  And unless you’ve truly gone down the tubes with those inherent mental health issues, no one gives seems to give you much moral support or encouragement, let alone congratulations, if you’re working on them.

By the way, speaking of drug problems, I was on constant opioids (including the dreaded fentanyl, the patch, in my case) for chronic pain for several years, .  I weaned myself off of them by myself, by my own choice, because I decided they were doing me more harm than good.  This is, of course, different from kicking an actual addiction—very different—but still, I have to try to find something about which I can brag.  Or wait, do I really have to do that?  Probably not.

I’m trying to do things to help myself mentally.  I’ve been reading a new (to me) book that deals with Adlerian psychology and philosophy, for instance.  So far it’s pretty good, but it’s not as insightful or useful (again, so far) as are things like Stoicism and Vipassana and the Tao Te Ching and so on.

I’m also trying to do more with brilliant dot org, which is a truly lovely app that can be used to study various STEM fields.  I did some problems on it in circuits yesterday—I had started that course months ago—but they are so far very basic.  There’s a lot of “drilling” on this app, but when it’s simple stuff it can get a bit tedious.  I guess that might be good.  Doing scales for piano practice is boring but very useful.

I want to get back into the math and science on the site.  I would love to complete every course they offer.  I would love to read every last bit of the textbooks and similar that I have in my mini-library at the office (I’ve added a few things since taking the latest picture).

I would love to learn everything that is learnable, to be honest, but to focus on the scientific before getting to things like literary and other criticism and such like.  As for political “science”, well…I think it’s probably still about at the stage of alchemy right now, and it may never get beyond that.

Unfortunately, my attention span is troublesome.  I get interested in one thing and/or idea and try to immerse myself in it, but then something distracts me soon enough, and some other interest draws me.  I do end up learning about a lot of esoteric subjects that way, though in bits and pieces**.  My ex-wife was always at least mildly annoyed by the number of books I had sitting on my bedside table, most either laid open or with numerous bookmarks.

Still, it would be good to do something until the “end” before moving on to the next thing.  At the very least, it would give me a sense of accomplishment.  I was doing that pretty well with my fiction, starting while I was a guest of the Florida DOC—I would finish a given book (or short story) completely, including editing and, once I was out, publishing before starting the next one.  This was a big deal, because my fiction writing used to suffer from the same issues of my scattered brain described above.

I have veered off that trajectory in recent years, alas.  I now have no fewer than three “begun” stories that I haven’t yet finished.  And no, I haven’t gotten any work done on any of them recently.  I’m too stressed out and worn out, and I am, at bottom, thoroughly alone here.  It’s really very difficult many days just to force myself to continue at all.  Also, disappointing and stupid events throughout the country and the world make that all the more difficult.

I hope you all are having a better time than I am.  I wish for you to be well, however useless such wishes may be.

P.S. Okay, well, if you look at (01-14-2026), you can make each of the digits of the year by adding digits of the month and date, without reusing any given month-date digit for any given year digit.  1 + 1 gives you the 2s, 0 gives you the 0, 4 + 1 + 1 gets you the 6.  That’s pretty lame though, even to me.

*I don’t know whether or not they are engaging posts (a phrase that sounds like an alternative expression for “hitching post”).

**Perhaps the fact that I seem to have to do things this way at least contributes to durability in my understanding, because I keep having to pick up where I left off months and even years ago.  Over time, I have gotten pretty good at being able to do that, and to be able very quickly, usually within the space of a paragraph or at most a page, to remember what was “going on” when I last was reading the book.  Yay, me.

by

How now, you secret, black, and midnight blogs!

Hello.  Good morning.

It’s Thursday.  It is, in fact, the 2nd Thursday in November, which means that, from the point of view of Thursdays in November, we are halfway to Thanksgiving (which in the US is the 4th Thursday in November).

Of course, we are not precisely halfway to Thanksgiving from the point of view of the days of the month of November overall.  Thanksgiving falls on the 27th of November this year‒14 days from today, of course‒so we are not quite halfway there as far as the days of November are concerned, but we are close to it.  If the month had started on a Friday, the halfway point in days versus Thursdays would be the same.

I think that the maximum disjunction would happen if the month began on a Thursday.  The 8th would then be the 2nd Thursday, and Thanksgiving would fall on the 22nd, which is quite a bit larger than 2 x 8.

Mind you, all this depends on starting one’s count in November.  That is not too unreasonable, but one could just as sensibly start counting Thursdays right at or after January 1st (let’s see, this year that’s 46/48 Thursdays, or about 95.833%).  If we did that, we would already be practically at Thanksgiving.  If we counted all days, we might be even closer still, percentage-wise.  Let’s see, 317/331, or about 95.770%.  Whataya know?  I was wrong, the Thursday one is “closer”.  I suspect this varies from year to year, but I’m not interested enough to check.

We could also begin our count at the beginning of autumn, which sort of seems appropriate.  Or, perhaps most sensibly still, we could start right after the previous Thanksgiving, beginning our counting on “Black Friday”.

Jeez Louise, I think I’m losing my mind, here.  Why am I writing about such nonsense?  I mean, yes, it’s interesting to notice how arbitrary and artificial human ways of counting days and things and so on are, so I suppose it’s somewhat edifying, and even could be mildly interesting for a moment.  But I nevertheless feel bad for wasting my readers’ time.

Though, I suppose, in a certain sense, one could say that all time is wasted‒“Plans that either come to naught or half a page of scribbled lines” and all that.

“Where do we come from?  The dust.  Where do we go to?  The grave.”

Of course, that last quote was not meant to be a general description of the human condition, but refers to Ray Bradbury’s “October People” in Something Wicked This Way Comes.  I’ve always thought that I’m an October person, since I was born in October.  Like Macduff, in the play from which Bradbury’s title above is taken, I was a C-section, though it would be a hyperbolic* to say that I was “ripped untimely” from the womb.  (Still, does my manner of birth mean I could defeat Macbeth?)

October is over now, in any case, and who** knows if I shall see another.

I don’t know if anyone has ever written about “November People”, but they don’t sound particularly scary nor particularly inspiring.  This assessment is not meant to refer to people born in November!  Several of my favorite people were born in November.

In other news, I did receive my Principles of Neural Science yesterday.  I used my dollar coins to choose a section, and I read it in the afternoon:  it was about neural firing and muscular activation during locomotion, briefly comparing lamprey with vertebrate, especially mammalian, locomotion patterns.

It may seem trivial, and I didn’t learn much that I didn’t at least implicitly know before, but the specifics are new, and all information has the potential to be useful.  We cannot know for certain ahead of time what knowledge might be most beneficial, just as we cannot predict the specifics of progress and invention.

As I said, I chose the textbook page via my coin-flipping process, using my three Sacagawea coins.  I keep a few dollar coins with Susan B. Anthony and/or the aforementioned Sacagawea with me at all times.

I carry such coins not so much for decision-making but because I like to roll them across my fingers when I want to “stop my hands feeling busy”.  I guess it’s a form of “stimming”, and I’ve been doing that particular one since college.  I taught myself to do it after I saw Val Kilmer, as Chris Knight, doing it in the movie Real Genius, which was one of my favorite movies.

Well, this has been a lot of pointless nonsense today, hasn’t it?  I apologize, and I guess I can try to mitigate my offense by at least trying not to produce too much of nothing***.  So I will draw this post to a close now.  I hope you all have a good day.  I will very likely write a post tomorrow, so you can look forward to that, if it’s the sort of thing to which you look forward.

TTFN

*You know, like non-Euclidean geometry.

**The WHO does not know, though with a bit of background information they could probably make reasonable predictions.

***According to the song, that can make a man feel ill at ease.  It can also, according to the same song, make a man abuse a king, which seems like it would be quite a rare situation.

by

“Though this be madness, yet there is method in’t”

Well, first let me apologize for yesterday’s blog that largely concerned the weather, and in a trivial sense at that.  It was rather lamentable, I know, with emphasis on the first four letters of that adjective.

On the other hand, I don’t apologize for having had my little bit of fun with the date.  That may have been even less interesting to most of you than my jabbering on about the weather, but I like it.  I fully expect that I will do such things again.  For instance, in a similar vein, today is a bit fun because it is 11-12*, so the numbers are in appropriate ordinal sequence with no gaps.

That’s not very fun.  More fun will be had (by me, anyway) on Friday, when it will be 11-14-25.  If you don’t immediately see the fun there, it may help that a similar fun date next month will be available on 12-13-25.  This fun also works with the European date order (but in both you have to leave out the digits that denote the century).  Also, there were no equivalently fun dates in any month before October.

This is the most fun I’ve had on any kind of date in at least 16 years, I would guess.  That’s an easy call, because I haven’t been on any date at all in at least that long.  See what I did there with the multiple meanings of the word “date”?  Of course you did.  What do I think you are, a moron?

No, I do not think that.  You are reading a blog post, so you are a reader, which gives you a serious leg-up, moronia-wise.  You draw from the well of that greatest of all human inventions:  written language.  Your taste in reading material may be somewhat questionable, but I cannot legitimately complain about that.

Wow, I feel like I ought to be almost done with this post, but I’ve barely passed 300 words.

On to other things.  I’m going to try to do a better job about science reading during my downtime in the office.  It’s not that I’m completely slacking; I’m reading Shape by mathematician Jordan Ellenberg, and I just read his earlier book How Not to Be Wrong.  I’ve read both before and/or listened to the audio books, but they are well worth rereading.  He’s a great math professor, and has a gift for explaining potentially abstract concepts.  I think he’s slightly better at this than Steven Strogatz, the author of The Joy of X and Infinite Powers, but they’re all good.

I also just yesterday gave in to an urge I’ve had for some time:  I ordered a textbook I liked in med school but which we didn’t really get into as deeply as I would like:  Principles of Neural Science, by Kandel et al.  The edition I had was by Kandel and Schwartz, if memory serves, but Dr. Schwartz is no longer involved, it seems.

It’s a textbook, so it’s pricey, even in paperback, but I discovered that I could put it on a payment plan through Amazon, so that’s what I did.  It arrives today.

I’ve also resolved, at least tentatively, to try to take the heat off my reading of my science books‒including the above newcomer‒by doing something I did when reviewing/studying in med school:  I would get a text that I was reviewing, and I would pick a section to read/review by flipping a coin.

Actually, it was a series of flips, each one dividing the “remaining” part of the book in half.  In other words, for the first flip, heads would mean I would look in the front half of the book, tails would mean the back half.  Then the next flip would decide to which half of that half I would narrow things down further.

Anyone who has spent any time dealing with computers and/or binary numbers can readily recognize that, with 10 flips of the coin, one could choose a specific page in a 1024 page book.  I guess every flip would count as a kind of “half-life” for the book’s pages.  If one wanted, one could even choose one’s pages not with a coin flip, which is not truly random, but with a quantum event that has a 50-50 chance, like measuring whether a given electron’s spin is up or down.

Of course, I don’t have a Stern-Gerlach gate, so I would have to “farm out” that process.  But I understand that there are apps that you can use that have their sources at labs where each decision is truly made by a quantum measurement.

It’s not terribly practical nor more useful for pickling book pages than is a coin flip, but if you’re a convinced advocate of the Everettian, “many worlds” version of quantum mechanics, it has the added “benefit” that each “flip” will divide the universe into two “worlds”, one where you choose from the earlier half, another where you choose from the latter.

Coin flips do not enact such splitting, not in anything but the trivial sense that every quantum level interaction potentially does so.  The experience will be the same for you, though, except whatever glee you might derive from splitting the universe to choose a section to read.

Anyway, I’ll be trying to read my books, random section by random section.  Believe it or not, this works for me.  I don’t have to learn things in order, usually, and this method avoids me feeling bored while trying to trudge through a text in order.

Perhaps I do have some aspects of ADHD up in there in my brain.

Well, I’ve now passed my target length for this post by some margin, so I’ll call this enough for today.  I expect to be writing another post tomorrow, but like everything else**, it is not absolutely certain.  I hope you have a very good day.

*Only in the American style Month-Day-Year format, though.  It is less fun in the European Day-Month-Year format.

**Yes, even death and taxes, in principle.

by

It’s a prime day for a (slightly) shorter blog post

Morning has broken!

Does anyone out there know a good, reasonably priced morning repair service or person?  I really don’t have the money or time to go pick out and buy a new morning.

Ha ha.

Sorry.  I know that’s quite a stupid joke.  Still, it should give you some idea just how tired I am.

I should have been able to get a decent sleep last night, but I did not.  That shouldn’t be anything new to me, but some days the effects of the insomnia seem to pile up far more than on some other days.  And today is one of those “pile up” days, it seems.

Thus, I intend to make this a relatively short blog post today if I can.  To that end, I’m setting my “target” number of words to be 701 instead of the usual 800*.  701 has the added advantage of being a prime number, which always makes things at least a little bit better from my point of view.

It’s funny how, as numbers get bigger, there seem to be fewer primes (they fall off as something like the natural log of the number range at which you’re looking, if memory serves).  And yet, there are an infinite number of them‒the same “countable infinity” as the natural numbers, “aleph nought”:

Also, we have the twin primes conjecture‒which apparently most mathematicians think is correct‒that there are an infinite number of primes that are with 2 of each other.

It has apparently been proven that there are an infinite number of primes separated by no more than about 500 or some such (it’s probably a lower separation now, but I haven’t looked into it in a while).  That may not seem like much of an accomplishment, but remember, we’re talking infinity here.  No matter how big the numbers get** you will never stop finding new sets of prime numbers that are no more than about 500 apart.

That’s not particularly useful to anyone but number theorists, I suppose, but it seems very interesting to me.

Incidentally, 701 is not part of a pair of twin primes, since 703 is not prime (it has four factors) and 699 is obviously divisible by 3.  And of course there is only one even prime (the number 2) because all other even numbers are divisible by 2.

Sorry, I know many people find these things boring, but I’m a fan of prime numbers.  In any case I’m trying not to be so negative in my blog posts, since I think it bothers a lot of people and may even be contagious at times.

It certainly doesn’t appear to do me any more good than does being a voice crying out in the wilderness, so to speak.  And despite the excellent biblical reference***, voices crying out in the wilderness usually are not heard or received by anyone or anything that can even understand them, let alone offer them any help.

I guess I can still talk about “imaginary” and complex numbers, because they just involve the square roots of negatives, but are not necessarily negative themselves****.  As long as I avoid multiplying them together, I should be able to steer relatively clear of negativity.

Ha ha, again.

I’m trying to try to avoid making other people miserable by expressing my own dark thoughts, so instead it seems I will make others miserable with my bad jokes.  You’re welcome.

Thinking about complex numbers makes me start feeling like I want to learn more about quaternions and spinors and so on, which seem truly fascinating, but about which I have only highly superficial knowledge.

It would be nice to learn more about them.  I probably will not, knowing me and my fatigued and distractible mind, but at least I can maybe be on the lookout for Numberphile videos about related subjects.  There’s at least one YouTube channel with a series on spinors.  Unfortunately, PBS Infinite Series stopped making new videos some time ago, but at least PBS Spacetime is still going strong, as are all of Brady Haran’s excellent channels.

And now, I’m over 701 (in the first draft), and so I’m done (for today at least).  I hope you all have a good day, and that your subsequent good days scale as the number of days, not as any logarithm thereof.

*I almost always go over my target, but at least it gives me a noteworthy place to decide it’s “time to wrap this up”.

**And there are described numbers so large that if you could memorize every digit of them, the information would be so concentrated as to turn your head into a black hole.

***It’s from the book of Isaiah.  John the Baptist supposedly quoted it and referred to himself as that voice, but then again, a lot of the writers of the “New Testament” shoehorned in references to supposed prophecy in the “Old Testament” to make the whole thing seem more sexy-cool (I guess).

****I just have to try to keep to the right upper quadrant of the complex plane.

by

Is an “almost” pair o’ dice just one die?

Oooooh, it’s Friday the 13th!  It’s so spooky!

Not really, of course.  It’s just a day.  I like Friday the 13ths, mostly just because so many people seem to imagine they are unlucky, though I think that superstition may be less prevalent now that it was in the past.  Nowadays, the day is probably mostly associated with the slasher film “series” that uses that title.  Not that even the original movie’s story ever had much to do with the day.  It just was a catchy, well-known “scary” day, following in the footsteps of Halloween (although the latter at least had a theme that suited the day).

Of course, a major reason I like this day is that the number 13 is a prime number, and I like prime numbers.  I like 13 especially, because 13 is possibly the most feared and reviled of the primes, associated with bad luck in much the way that 7 is associated with good luck.

Hmm.  I know at least part of 7’s appeal probably has to do with the dice game “craps”.  7 is the most common total to achieve when rolling two six-sided dice, because there are more ways to get that total than any other number.  Meanwhile, of course, there is no way to get a 13 on two (normally numbered) six-sided dice, but it is only just out of reach.  It’s the first number that’s too high for such a pair o’ dice*.

Of course, you can’t roll a 1 on two six-sided dice either, but that feels more trivial.

I honestly don’t think the reason for 13’s association with bad luck probably has anything to do with dice; it wouldn’t make too much sense.  But someone out there, please correct me if I’m wrong.

It’s interesting to think about probability regarding dice, not least because the very field of probability theory was first created by a guy who wanted to optimize his chances of winning at dice.  According to what I’ve read, he succeeded, at least temporarily.

Nowadays, of course, that field has grown into a special subset of mathematics and physics and information theory and so on, affecting everything from thermodynamics and statistical mechanics to meteorology and quantum mechanics.  In a certain sense‒given that Schrodinger’s equation describes wave functions that have to be squared (in a complex conjugate way) to get literal probabilities that, based on Bell’s Theorem, cannot be further simplified, as far as we know‒probability may be something truly fundamental to the universe, not merely a tool for situations in which we don’t have access to information.  Based on Bell’s Theorem, which has been shown to apply in the Nobel Prize winning experiments of Aspect et al, it seems that, at root, as far as we can tell, the quantum mechanical operations are fundamentally indeterministic.

Of course, just because something is “random” at a lower level doesn’t imply that, at higher levels of organization, it can’t behave in ways that are very much deterministic in character.  Lots of little things behaving in a locally random manner can combine to create inevitable larger-scale behavior.  Perhaps the most straightforward and compelling such thing is the behavior of gases and the Ideal Gas Law***.  The motion of any given molecule of gas is unpredictable‒at the very least it is stochastic and has so many degrees of freedom as to be unpredictable in practice, but since quantum mechanics is involved in intermolecular collisions, it may truly be random in its specifics.

And yet, when oodles and oodles of molecules of a gas come together****, their collective behavior can be so utterly consistent‒with very little depending on even what kinds of molecules comprise the gas‒as to produce a highly accurate “law” with only 4 variables, one constant, and no exponents!

If that doesn’t seem remarkable to you, either you’re jaded because you’ve known it since secondary school or I haven’t explained it very well (or both, of course).

It’s interesting to think about the probabilities of dice games using more than two dice and/or dice with more or fewer than six sides.  Tabletop role-playing gamers will know that in addition to the 5 “perfect” Platonic solids*****, there are quite a few other symmetrical (but with sides not formed from “regular” polygons) solid shapes that can be turned into everything from ten-sided to thirty-sided dice.

But RPGs tend to involve rolling one die at a time, except when rolling up characters, at which time (in D and D and Gamma World, at least) one uses 3 six-sided dice (or 4 when applying a technique to yield better-than-average characters).

I wonder why there are no games of chance using more than 3 six-sided dice or using, say, multiple four-sided dice or eight- or twenty- or twelve-sided dice.  The probabilities would be more trouble to work out, but they would not be harder in principle.  If any of you out there either know of or want to invent a game of chance using more than 2 dice and/or other than six-sided dice, feel free to share below.

In the meantime, I’ll call this enough for today.  I am supposed to work tomorrow as far as I know, though that’s always subject to change.  If there’s no post here tomorrow, then it probably means I didn’t work.  I probably will work, though I couldn’t give you a rigorous working out of the mathematics involved in determining that particular probability.

Have a good day if you’re able.

*You can sometimes see them by the dashboard lights.

**Unless superdeterminism is correct.  However, this is a very hypothetical thing, and I’m not very familiar with what arguments are proposed to support it, so I won’t get into it.

***PV = nRT if memory serves. [Looks it up]  Yep, that’s right.  Four variables and one constant (R).

****Even if it’s not right now, over me.

*****These are, presumably, solids that really care about each other but in a non-romantic way.